About dither, on a practical level
Quote from Pedja on 28 July 2025, 9:45 PMAs I promised a few weeks ago, here are my results with dither listening. I did my best to come up with some reliable information and pointers, but you should consider this an ongoing work, because the possible options in this area are not limited to the ones I tried.
But first, let me try to be inclusive with this article, so for those possibly new to dither, a short intro.
Dither, which is essentially the noise added during the A/D conversion or bit-depth reduction, has two effects. First, it breaks the firm relation between the signal and the quantization artifacts, and second, it makes it possible to reproduce signal levels below the LSB level.
In our case, if we use 24-bit sources with the TDA1541(A) DAC, even though it can normally work with such sources and truncate everything after 16th bit, we could also try to apply the dither before D/A conversion, to overcome the intrinsic 16-bit performance possibly, and also try to avoid loosing the 8 bottom bits of 24-bit sources when converted by our 16-bit converter.
My main concern will remain the first of these two effects, and for now I will set aside the importance of the signals below the LSB (for a 16-bit system, it is -90.3 dBFS), even though this feature is directly linked to the original invention of dither.
Speaking about this, historically, the invention of dither happened in the aircraft industry, almost a century ago, when engineers noted that control systems worked more precisely and were able to recognize lower-level objects if mounted on the aircraft, which is the vibrational ("noisy") environment, than if they were on steady ground. In the audio, the first explicit proposal for dither, to my knowledge, came from Vanderkooy and Lipschitz in 1984. I am not sure if their article is anywhere available freely online, but Leon Melkonian’s 1992 article for National (now part of the Texas Instruments), Improving A/D converter performance using dither, should be also useful, witnessing on the initial expectations of this technique in the early days of the digital audio.
Anyhow, I will limit myself here to the dither ability to break the relation between the signal and the artifacts, for now ignoring its feature of playing the levels below the LSB.
So, in my case, I used two Foobar2000 plugins, MDA Dither and Smart Dither, to reduce the 24-bit sources to 16-bit. They both offer TPDF dither (Triangular Probability Density Function), and both provide the option of high-pass noise shaping. In addition, the MDA Dither plugin offers the second-order dither, which, in itself, integrates a noise shaper. Nominally, both these plugins can perform the dither at up to 4 (lower) bits, however, they differ in the way they scale the dither amplitude and are not directly comparable in this regard.
I am by no means an expert in dither algorithms, and I am not sure how these two plugins differ in their basic code (according to some, they both might originate from the old MDA plugin for the VST - Virtual Studio Technology platform), but the implementations are apparently somewhat different.
I both measured the effects of these processes and listened to some particular recordings for some time.
As I promised a few weeks ago, here are my results with dither listening. I did my best to come up with some reliable information and pointers, but you should consider this an ongoing work, because the possible options in this area are not limited to the ones I tried.
But first, let me try to be inclusive with this article, so for those possibly new to dither, a short intro.
Dither, which is essentially the noise added during the A/D conversion or bit-depth reduction, has two effects. First, it breaks the firm relation between the signal and the quantization artifacts, and second, it makes it possible to reproduce signal levels below the LSB level.
In our case, if we use 24-bit sources with the TDA1541(A) DAC, even though it can normally work with such sources and truncate everything after 16th bit, we could also try to apply the dither before D/A conversion, to overcome the intrinsic 16-bit performance possibly, and also try to avoid loosing the 8 bottom bits of 24-bit sources when converted by our 16-bit converter.
My main concern will remain the first of these two effects, and for now I will set aside the importance of the signals below the LSB (for a 16-bit system, it is -90.3 dBFS), even though this feature is directly linked to the original invention of dither.
Speaking about this, historically, the invention of dither happened in the aircraft industry, almost a century ago, when engineers noted that control systems worked more precisely and were able to recognize lower-level objects if mounted on the aircraft, which is the vibrational ("noisy") environment, than if they were on steady ground. In the audio, the first explicit proposal for dither, to my knowledge, came from Vanderkooy and Lipschitz in 1984. I am not sure if their article is anywhere available freely online, but Leon Melkonian’s 1992 article for National (now part of the Texas Instruments), Improving A/D converter performance using dither, should be also useful, witnessing on the initial expectations of this technique in the early days of the digital audio.
Anyhow, I will limit myself here to the dither ability to break the relation between the signal and the artifacts, for now ignoring its feature of playing the levels below the LSB.
So, in my case, I used two Foobar2000 plugins, MDA Dither and Smart Dither, to reduce the 24-bit sources to 16-bit. They both offer TPDF dither (Triangular Probability Density Function), and both provide the option of high-pass noise shaping. In addition, the MDA Dither plugin offers the second-order dither, which, in itself, integrates a noise shaper. Nominally, both these plugins can perform the dither at up to 4 (lower) bits, however, they differ in the way they scale the dither amplitude and are not directly comparable in this regard.
I am by no means an expert in dither algorithms, and I am not sure how these two plugins differ in their basic code (according to some, they both might originate from the old MDA plugin for the VST - Virtual Studio Technology platform), but the implementations are apparently somewhat different.
I both measured the effects of these processes and listened to some particular recordings for some time.
Quote from Pedja on 30 July 2025, 6:20 PMS5 DAC performance with undithered and dithered signals
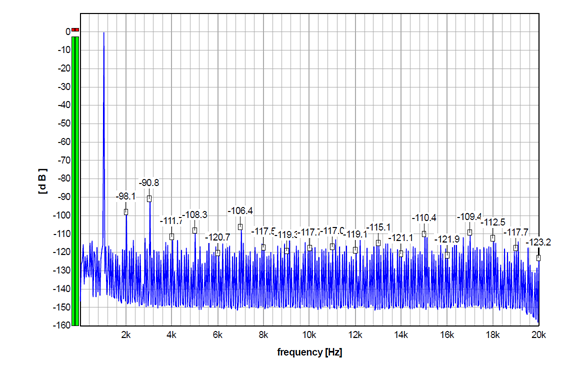
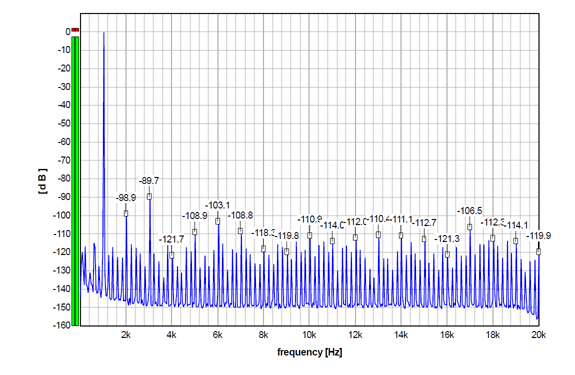
So, first, the graphs. Below, you will see the FFT graphs for a 24-bit 1 kHz sinewave, sampled at 44.1 kHz, played by the Audial S5 DAC, without and with several dither options. It is the original S5, my prototype sample, and not S5b, but the results would be similar with S5b too.
The first graph shows a 24-bit 1 kHz sinewave, without dither, normally truncated during conversion to 16 bits. THD=0.0034%.
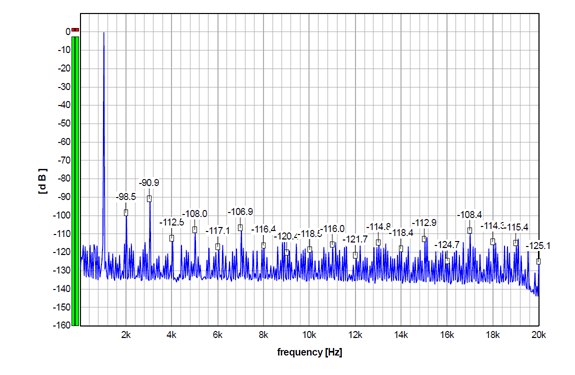
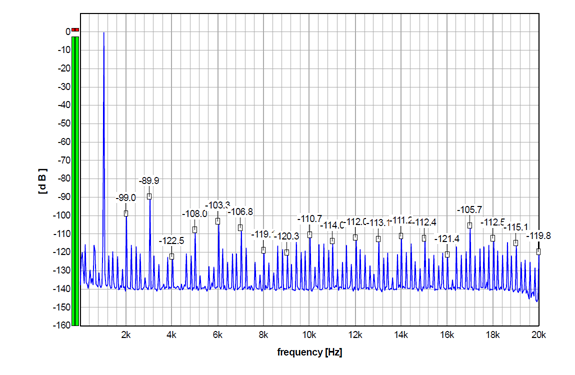
The next three graphs show the same 24-bit 1 kHz sinewave, now dithered down to 16 bits by the MDA plugin, operating at the 2 lowest bits. The first graph shows TPDF dither. THD=0.0034%, THD+N=0.0045%. For the record, here you can see the same dither applied to the 3 bits, which apparently increased the noise floor for 3 dB or so.
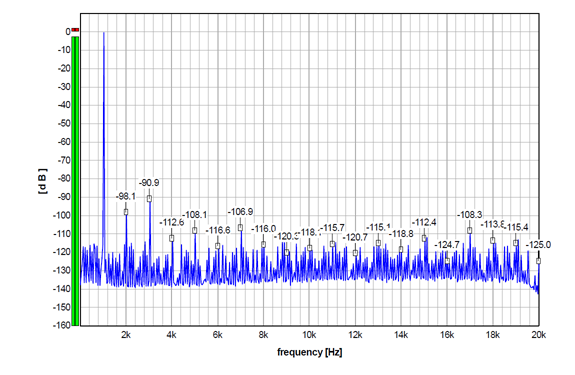
And then the same TPDF as above, so it is applied to 2 LSB, but now with a high-pass noise filter. A high-pass is clearly visible in the noise floor, although it is not very strong. THD and THD+N remain the same as above.
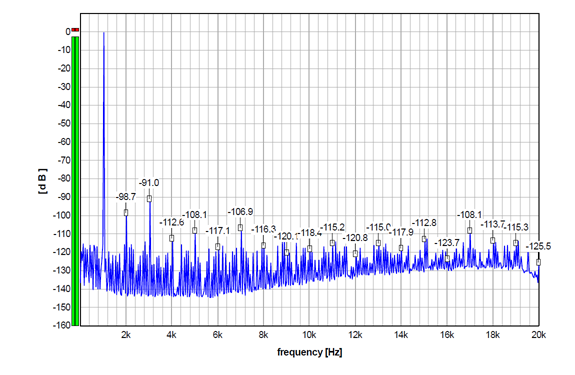
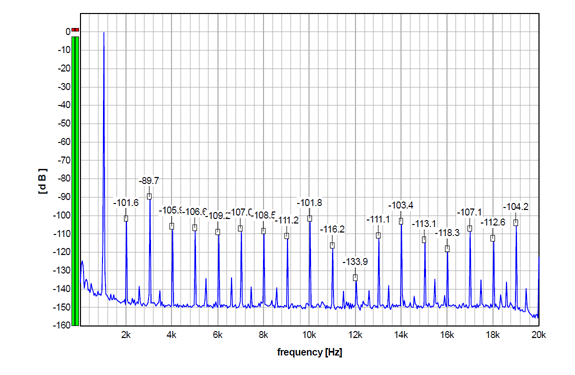
And, the second-order dither. As such, it includes noise shaping, and it is obviously stronger than the one above. THD=0.0034%, THD+N=0.0048%. (My side note here is that this dither looks most similar to that I use for measurements for decades, and which is actually a TPDF dither, with noise shaped towards the Fletcher-Munson curve. It was generated by a different software, though.)
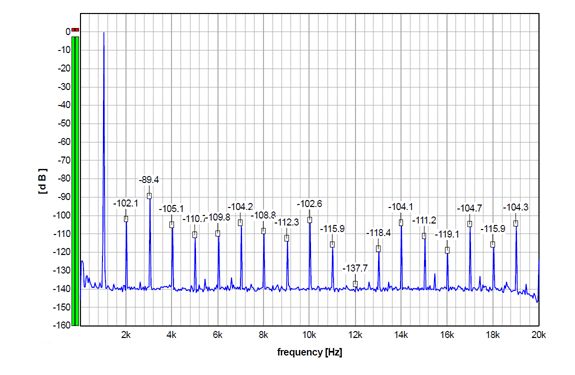
I also checked the behaviour with the Smart Dither plugin, and when I set it to 1 LSB, the graphs looked practically the same as the MDA Dither plugin set to 2 LSB. As I already said, Smart Dither offers TPDF dither only.
So, all the graphs above show practically the same distortion performance for non-dithered and dithered signals. The differences visible in some harmonics are within the usual fluctuations when measuring this device. So the main contributor to the distortion components in all these graphs is apparently the DAC itself (including this DAC output stage, of course).
Consequently, in this case, the dither apparently can not improve the distortion figure here. To improve on it, an improvement on the DAC intrinsic performance would be most probably required.
Some may notice that, when investigating the relation between the dither and the distortion performance, it might be more natural to use lower-level signals. I actually did make all these measurements with -60 dBFS signals too, however, the conclusions were the same, so no sense in posting them too.
So, technically speaking, what the dither changes here is the noise floor in the first place.
S5 DAC performance with undithered and dithered signals
So, first, the graphs. Below, you will see the FFT graphs for a 24-bit 1 kHz sinewave, sampled at 44.1 kHz, played by the Audial S5 DAC, without and with several dither options. It is the original S5, my prototype sample, and not S5b, but the results would be similar with S5b too.
The first graph shows a 24-bit 1 kHz sinewave, without dither, normally truncated during conversion to 16 bits. THD=0.0034%.
The next three graphs show the same 24-bit 1 kHz sinewave, now dithered down to 16 bits by the MDA plugin, operating at the 2 lowest bits. The first graph shows TPDF dither. THD=0.0034%, THD+N=0.0045%. For the record, here you can see the same dither applied to the 3 bits, which apparently increased the noise floor for 3 dB or so.
And then the same TPDF as above, so it is applied to 2 LSB, but now with a high-pass noise filter. A high-pass is clearly visible in the noise floor, although it is not very strong. THD and THD+N remain the same as above.
And, the second-order dither. As such, it includes noise shaping, and it is obviously stronger than the one above. THD=0.0034%, THD+N=0.0048%. (My side note here is that this dither looks most similar to that I use for measurements for decades, and which is actually a TPDF dither, with noise shaped towards the Fletcher-Munson curve. It was generated by a different software, though.)
I also checked the behaviour with the Smart Dither plugin, and when I set it to 1 LSB, the graphs looked practically the same as the MDA Dither plugin set to 2 LSB. As I already said, Smart Dither offers TPDF dither only.
So, all the graphs above show practically the same distortion performance for non-dithered and dithered signals. The differences visible in some harmonics are within the usual fluctuations when measuring this device. So the main contributor to the distortion components in all these graphs is apparently the DAC itself (including this DAC output stage, of course).
Consequently, in this case, the dither apparently can not improve the distortion figure here. To improve on it, an improvement on the DAC intrinsic performance would be most probably required.
Some may notice that, when investigating the relation between the dither and the distortion performance, it might be more natural to use lower-level signals. I actually did make all these measurements with -60 dBFS signals too, however, the conclusions were the same, so no sense in posting them too.
So, technically speaking, what the dither changes here is the noise floor in the first place.
Quote from Pedja on 9 August 2025, 11:52 AMSonic properties of a dither
The listening was more interesting, less predictable, and less simple. And here, in some way, it stretched my abilities to define the differences and make decisions. The recordings I listened to were all 24-bit, including "You Want it Darker" by Leonard Cohen, "The Visitor" by Kadhja Bonet, "Skeleton Tree" by Nick Cave, and "The Last Dance" by Keith Jarrett and Charlie Haden. All these were 44.1 or 48 kHz sampling rate, but I also tried Olafur Arnalds' "re:member" (24/96), as well as several classic recordings in DXD format (24/352.8).
I listened first to the MDA plugin set to TPDF (to reduce the word length to 16 bits), and what it brought was somewhat more precise positioning, but less bodied tone, and with somewhat reduced dynamics.
Adding high-pass noise shaping further widened the soundstage, generally increasing it in space.
Using second-order dither apparently boosted all the effects I already noticed with TPDF dither and HP noise shaper.
The MDA plugin now also has the option to "leave digital silence undithered", and I am not sure about the way it really works, but I got the impression that, when I enabled this option, the fullness got less compromised.
I also listened to the Smart Dither plugin. As I already noted, I am not sure how their algorithms differ, but, all else being equal, so with Smart Dither (TPDF) set to 1 LSB (Smart Dither set to 1 LSB is equivalent to MDA Dither set to 2 LSB, which is how I mostly used it) and with noise shaper turned on, I think I preferred it sonically to MDA. This is because, similar to MDA, it brings more precise soundstaging, but it remains tonally more neutral, with no loss of dynamics. However, I still noticed some loss of resolution in the mid part of the bass.
Generally, what I missed while listening to any of these two dither plugins, at any setting, was the system's ability to reach some tonally velvety moments effortlessly, and a certain lack of a very particular sense of breath. This last remark is not easy to clarify, because dither does not compromise transparency; it is quite the opposite, I think it even improves it.
So, for me, this remained a sort of something lost – something found case. I think I could personally live without dither, but I would strongly recommend everyone who has the option to try this and draw their conclusions, based on their system and sonic priorities. The differences probably won't be huge, but should be perceivable.
But I hope these posts provide good and reliable starting points.
As I mentioned, I also checked the dither effects by listening to some recordings with higher sampling frequencies, and the conclusions were similar.
However, as I find the relation between sampling frequency and the error signal also important, I will post more about it shortly.
Sonic properties of a dither
The listening was more interesting, less predictable, and less simple. And here, in some way, it stretched my abilities to define the differences and make decisions. The recordings I listened to were all 24-bit, including "You Want it Darker" by Leonard Cohen, "The Visitor" by Kadhja Bonet, "Skeleton Tree" by Nick Cave, and "The Last Dance" by Keith Jarrett and Charlie Haden. All these were 44.1 or 48 kHz sampling rate, but I also tried Olafur Arnalds' "re:member" (24/96), as well as several classic recordings in DXD format (24/352.8).
I listened first to the MDA plugin set to TPDF (to reduce the word length to 16 bits), and what it brought was somewhat more precise positioning, but less bodied tone, and with somewhat reduced dynamics.
Adding high-pass noise shaping further widened the soundstage, generally increasing it in space.
Using second-order dither apparently boosted all the effects I already noticed with TPDF dither and HP noise shaper.
The MDA plugin now also has the option to "leave digital silence undithered", and I am not sure about the way it really works, but I got the impression that, when I enabled this option, the fullness got less compromised.
I also listened to the Smart Dither plugin. As I already noted, I am not sure how their algorithms differ, but, all else being equal, so with Smart Dither (TPDF) set to 1 LSB (Smart Dither set to 1 LSB is equivalent to MDA Dither set to 2 LSB, which is how I mostly used it) and with noise shaper turned on, I think I preferred it sonically to MDA. This is because, similar to MDA, it brings more precise soundstaging, but it remains tonally more neutral, with no loss of dynamics. However, I still noticed some loss of resolution in the mid part of the bass.
Generally, what I missed while listening to any of these two dither plugins, at any setting, was the system's ability to reach some tonally velvety moments effortlessly, and a certain lack of a very particular sense of breath. This last remark is not easy to clarify, because dither does not compromise transparency; it is quite the opposite, I think it even improves it.
So, for me, this remained a sort of something lost – something found case. I think I could personally live without dither, but I would strongly recommend everyone who has the option to try this and draw their conclusions, based on their system and sonic priorities. The differences probably won't be huge, but should be perceivable.
But I hope these posts provide good and reliable starting points.
As I mentioned, I also checked the dither effects by listening to some recordings with higher sampling frequencies, and the conclusions were similar.
However, as I find the relation between sampling frequency and the error signal also important, I will post more about it shortly.
Quote from Pedja on 10 August 2025, 12:23 PMSampling frequency and the amplitude domain
So, I believe the relationship between the sampling frequency and error in the amplitude domain should also be considered. Namely, today we can use our beloved 16-bit TDA1541(A) D/A converter chip with sampling frequencies notably higher than 44.1 kHz, and since the overall resolution is a sort of product of the time and amplitude domain, that may also bring a different perspective on the amplitude behavior, and on all the techniques associated with it, including the dither. In other words, higher sampling frequencies not only improve the time-domain performance and reduce the HF mirror images' levels. They also improve the amplitude behavior, as they make the PCM raster more precise, effectively in both axes, with the given waveform.
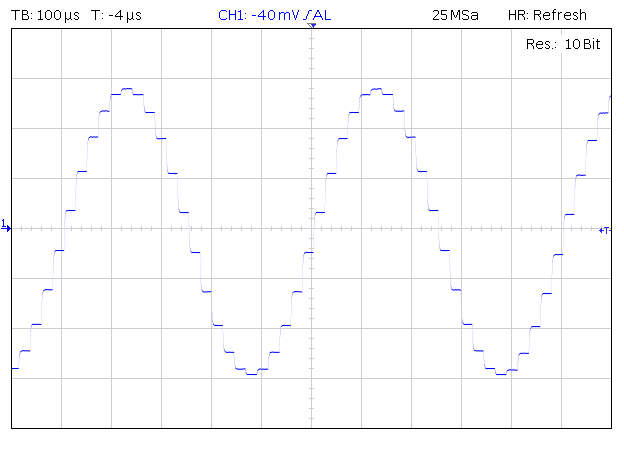
So, consider the scope shots of two 2 kHz sinewaves, sampled at 44.1 kHz and 192 kHz, respectively. I used 2 kHz here instead of the usual 1 kHz, to lower the number of available samples, and thus show the difference more obviously. This is again Audial S5, so a non-oversampling DAC, showing the original waveform, as is.
The number of available levels for the amplitude rounding, of course, remains the same (65,536 for 16 bits), and the quantization error overall level actually remains the same, too; however, it gets distributed evenly across the Nyquist bandwidth (Fs/2), leaving the audio band itself more clean.
Going back to 1 kHz, the graph below shows an undithered 1 kHz sinewave with Fs 176.4 kHz (it is 24-bit, normally truncated to 16 bits), again run through my Audial S5 prototype. Please compare this graph with the first one above. Harmonically related components are similar, but the amount and the level of the other discrete artifacts is lower.
With dither, it looks like this. It should be compared to the second graph above. Please note that, with higher Fs, the dithered signal noise floor also gets lower.
For the record, here is the S5 performance with 24-bit (undithered/truncated) 1 kHz sinewave sampled at Fs 192 kHz, which is a multiple of the sampled 1 kHz signal, so there is a whole number of samples per oscillation. Almost all the discrete components, apart from the harmonics, practically disappeared, so we can verify that non-harmonically related discrete artifacts in the graphs above are not produced by the DAC, but by the source signal itself.
And, the same 1 kHz @ Fs 192 kHz, with dither.
So, once we increase the sampling frequency, the general rule for the quantization error of the digital system, given by 1.76 + 6.02 x n (in dB), or for the dynamic range simply given by 2^n, where n is the number of available bits, becomes insufficient, or at least not informative enough, unless it is expressed in the frequency domain.
These phenomena were well known to early oversampling designers back in the 80s, and the whole concept of the sigma/delta conversion, which started ruling the audio industry soon afterwards, achieves the resolution and linearity by the increased sampling frequency and associated noise shaping, hugely abandoning precise conversion in the actual amplitude domain at that.
No one here probably wants to involve sigma/delta modulation here, but it will probably be good to also sketch the options we have with different sampling frequencies, bit lengths, and dither, by using a classic multibit 16-bit converter. So please stay tuned for one more post.
Sampling frequency and the amplitude domain
So, I believe the relationship between the sampling frequency and error in the amplitude domain should also be considered. Namely, today we can use our beloved 16-bit TDA1541(A) D/A converter chip with sampling frequencies notably higher than 44.1 kHz, and since the overall resolution is a sort of product of the time and amplitude domain, that may also bring a different perspective on the amplitude behavior, and on all the techniques associated with it, including the dither. In other words, higher sampling frequencies not only improve the time-domain performance and reduce the HF mirror images' levels. They also improve the amplitude behavior, as they make the PCM raster more precise, effectively in both axes, with the given waveform.
So, consider the scope shots of two 2 kHz sinewaves, sampled at 44.1 kHz and 192 kHz, respectively. I used 2 kHz here instead of the usual 1 kHz, to lower the number of available samples, and thus show the difference more obviously. This is again Audial S5, so a non-oversampling DAC, showing the original waveform, as is.
 |
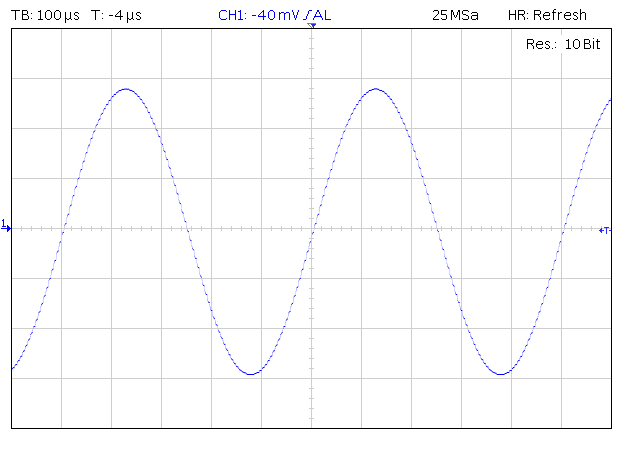 |
The number of available levels for the amplitude rounding, of course, remains the same (65,536 for 16 bits), and the quantization error overall level actually remains the same, too; however, it gets distributed evenly across the Nyquist bandwidth (Fs/2), leaving the audio band itself more clean.
Going back to 1 kHz, the graph below shows an undithered 1 kHz sinewave with Fs 176.4 kHz (it is 24-bit, normally truncated to 16 bits), again run through my Audial S5 prototype. Please compare this graph with the first one above. Harmonically related components are similar, but the amount and the level of the other discrete artifacts is lower.
With dither, it looks like this. It should be compared to the second graph above. Please note that, with higher Fs, the dithered signal noise floor also gets lower.
For the record, here is the S5 performance with 24-bit (undithered/truncated) 1 kHz sinewave sampled at Fs 192 kHz, which is a multiple of the sampled 1 kHz signal, so there is a whole number of samples per oscillation. Almost all the discrete components, apart from the harmonics, practically disappeared, so we can verify that non-harmonically related discrete artifacts in the graphs above are not produced by the DAC, but by the source signal itself.
And, the same 1 kHz @ Fs 192 kHz, with dither.
So, once we increase the sampling frequency, the general rule for the quantization error of the digital system, given by 1.76 + 6.02 x n (in dB), or for the dynamic range simply given by 2^n, where n is the number of available bits, becomes insufficient, or at least not informative enough, unless it is expressed in the frequency domain.
These phenomena were well known to early oversampling designers back in the 80s, and the whole concept of the sigma/delta conversion, which started ruling the audio industry soon afterwards, achieves the resolution and linearity by the increased sampling frequency and associated noise shaping, hugely abandoning precise conversion in the actual amplitude domain at that.
No one here probably wants to involve sigma/delta modulation here, but it will probably be good to also sketch the options we have with different sampling frequencies, bit lengths, and dither, by using a classic multibit 16-bit converter. So please stay tuned for one more post.
Quote from Pedja on 11 August 2025, 12:09 PMSo, where are the hypothetical limits of a 16-bit system, really?
In this PCM digital audio, looking inside the audio band, we can generally distinguish three kinds of artifacts, intrinsic to the process. The first are harmonically related components, so it's the same old harmonic distortion. The second is the myriad of discrete artifacts, which appear because the sampling frequency and sampled signal are not harmonically related. And then, once we apply dither, we also have the wideband noise. Normally, a classic signal without a dither has the first two, while a dithered signal has all these artifacts.
All the graphs above show the real-world behavior of the system with the given signals, however harmonically related components are dominated and thus masked by the DAC itself. Hence, the following graphs show the spectral analysis of a 1 kHz sinewave, sampled at different sampling and bit rates, without and with dither, and the analysis shows these files as such, so without hardware involved, to demonstrate the theoretical limits for each approach. To avoid different distribution of discrete artifacts, I compared the quantization error for 44.1 kHz and 176.4 kHz (and not 192 kHz) sampling frequency.
So, first 1 kHz sinewave, 16-bit, sampled at 44.1 kHz and 176.4 kHz, respectively, and no hardware involved, just the files analyzed. As in the measurement graphs above, a higher sampling frequency again shows the same level for harmonic-related artifacts, but significantly less other discrete artifacts. So, while the harmonic distortion remains the same, the nominal improvement in SNR for 4 times higher Fs is 6 dB, and at 352.8 kHz, it would be 9 dB.
Then, 1 kHz sinewave, 24-bit, sampled at 44.1 kHz and 176.4 kHz.
And finally, the same 24-bit, Fs 44.1 kHz and Fs 176.4 kHz files, dithered down to 16-bit, by TPDF dither, performed at 2 LSB, and noise shaped (44.1 kHz file according to the Fletcher-Munson curve; I generated these files by using the ancient Sonic Foundry Sound Forge, and not Foobar2000 and its plugins).
Obviously, by using a higher sampling frequency, and by breaking the dependence between the signal and error by the use of dither, this last option goes way beyond anything usually associated with "16-bit performance". I would personally like to hear the system that includes a good dither algorithm and hardware that can fulfill, or at least get close to, such requirements. What I am sure of is that the TDA1541A can not do this, and it, in addition, puts some constraints regarding the surrounding design i.e. the output stage (unless the opamp I/V is fine with you), which makes things even harder.
Taking into account that the DACs are usually not made even to meet the nominal performance for their given number of bits, this would be a historically new situation, where the DAC should outperform it. And then everyone should also decide for themselves if it makes much sense or not. I personally once might try making such a 16-bit converter (it must be some custom, discrete design, of course), but please, do not hold your breath.
So, where are the hypothetical limits of a 16-bit system, really?
In this PCM digital audio, looking inside the audio band, we can generally distinguish three kinds of artifacts, intrinsic to the process. The first are harmonically related components, so it's the same old harmonic distortion. The second is the myriad of discrete artifacts, which appear because the sampling frequency and sampled signal are not harmonically related. And then, once we apply dither, we also have the wideband noise. Normally, a classic signal without a dither has the first two, while a dithered signal has all these artifacts.
All the graphs above show the real-world behavior of the system with the given signals, however harmonically related components are dominated and thus masked by the DAC itself. Hence, the following graphs show the spectral analysis of a 1 kHz sinewave, sampled at different sampling and bit rates, without and with dither, and the analysis shows these files as such, so without hardware involved, to demonstrate the theoretical limits for each approach. To avoid different distribution of discrete artifacts, I compared the quantization error for 44.1 kHz and 176.4 kHz (and not 192 kHz) sampling frequency.
So, first 1 kHz sinewave, 16-bit, sampled at 44.1 kHz and 176.4 kHz, respectively, and no hardware involved, just the files analyzed. As in the measurement graphs above, a higher sampling frequency again shows the same level for harmonic-related artifacts, but significantly less other discrete artifacts. So, while the harmonic distortion remains the same, the nominal improvement in SNR for 4 times higher Fs is 6 dB, and at 352.8 kHz, it would be 9 dB.
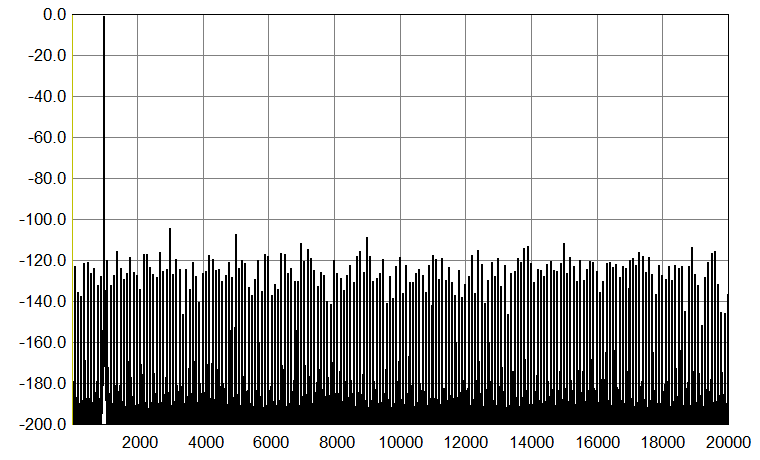 |
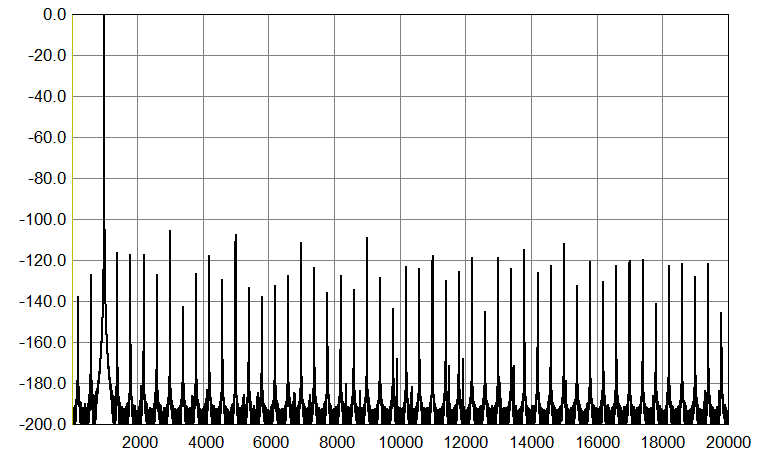 |
Then, 1 kHz sinewave, 24-bit, sampled at 44.1 kHz and 176.4 kHz.
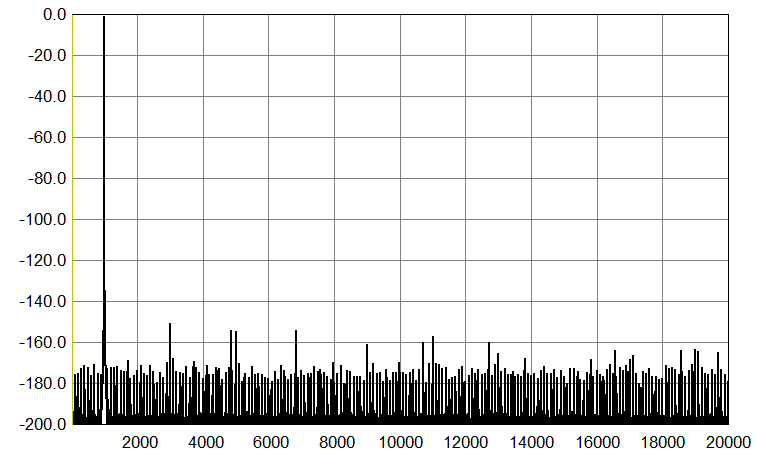 |
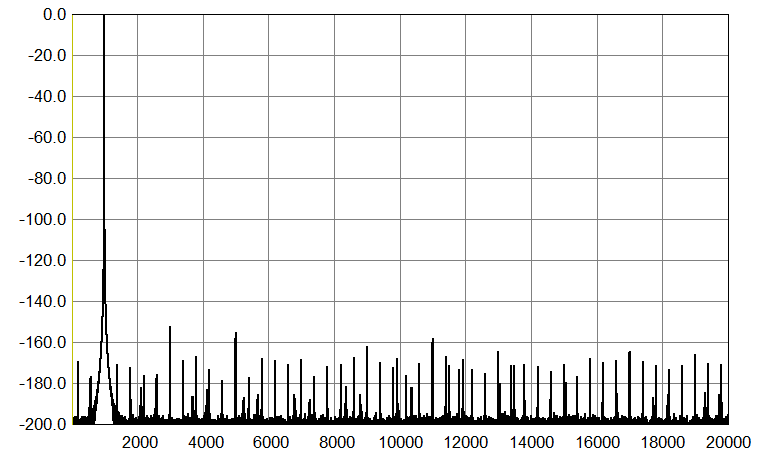 |
And finally, the same 24-bit, Fs 44.1 kHz and Fs 176.4 kHz files, dithered down to 16-bit, by TPDF dither, performed at 2 LSB, and noise shaped (44.1 kHz file according to the Fletcher-Munson curve; I generated these files by using the ancient Sonic Foundry Sound Forge, and not Foobar2000 and its plugins).
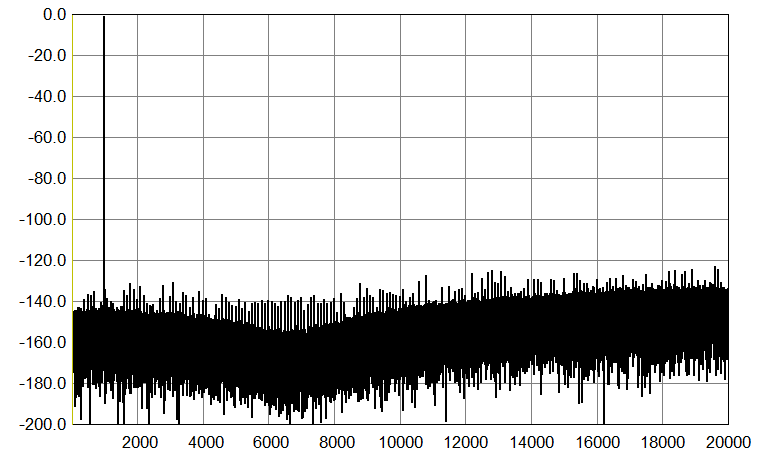 |
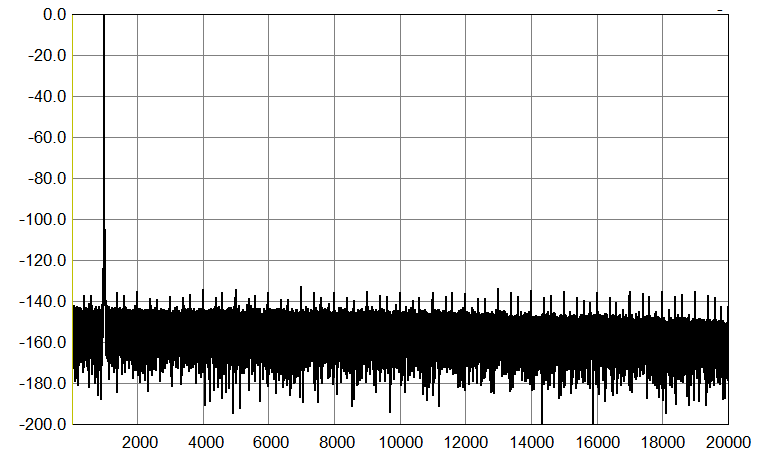 |
Obviously, by using a higher sampling frequency, and by breaking the dependence between the signal and error by the use of dither, this last option goes way beyond anything usually associated with "16-bit performance". I would personally like to hear the system that includes a good dither algorithm and hardware that can fulfill, or at least get close to, such requirements. What I am sure of is that the TDA1541A can not do this, and it, in addition, puts some constraints regarding the surrounding design i.e. the output stage (unless the opamp I/V is fine with you), which makes things even harder.
Taking into account that the DACs are usually not made even to meet the nominal performance for their given number of bits, this would be a historically new situation, where the DAC should outperform it. And then everyone should also decide for themselves if it makes much sense or not. I personally once might try making such a 16-bit converter (it must be some custom, discrete design, of course), but please, do not hold your breath.